Los Polígonos

Polígono

Un polígono es una figura plana (bidimensional) cerrada con lados rectos. Algunos ejemplos son triángulos, cuadriláteros, pentágonos, hexágonos, etc.

Regular

Un "polígono regular" tiene todos los lados iguales y todos los ángulos iguales. Si no, es irregular.

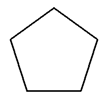Pentágono regular	Pentágono irregular

Ángulo interior El ángulo interior de un polígono regular de "n" lados se calcula con la fórmula: (n-2) × 180° / n Por ejemplo el ángulo interior de un octágono (8 lados) es: (8-2) × 180° / 8 = 6×180°/8 = 135° Y el de un cuadrado es (4-2) × 180° / 4 = 2×180°/4 = 90°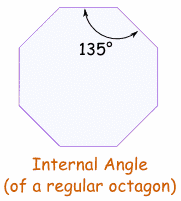

Ángulo exterior Los ángulos exterior e interior se miden sobre la misma línea, así que suman 180°. Por lo tanto el ángulo exterior es simplemente 180° - ángulo interior El ángulo interior de este octágono es 135°, así que el ángulo exterior es 180°-135° = 45° El ángulo interior de un hexágono es 120°, así que el ángulo exterior es 180°-120° = 60°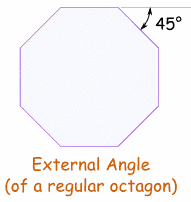

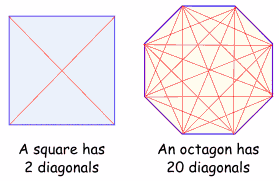Diagonales Todos los polígonos (menos los triángulos) tienen diagonales (líneas que van de un vértice a otro, pero que no son lados). El número de diagonales es n(n - 3) / 2. Ejemplos: un cuadrado tiene 4(4-3)/2 = 4×1/2 = 2 diagonales un octágono tiene 8(8-3)/2 = 8×5/2 = 20 diagonales (Nota: esto vale para polígonos regulares e irregulares)

Circunferencia inscrita, circunscrita, radio y apotema

"Circunferencia inscrita, circunscrita, radio y apotema ... "

Suena musical si lo repites unas cuantas veces, pero sólo son los nombres de los círculos "exterior" e "interior" (y sus radios) que se pueden dibujar en un polígono regular, así:

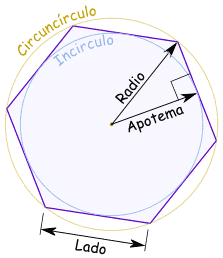La circunferencia "exterior" se llama circunscrita (a veces también "circuncírculo"), y conecta los vértices del polígono. La circunferencia "interior" se llama inscrita (a veces también "incírculo"), y toca cada lado del polígono en el punto medio. El radio de la circunferencia circunscrita es también el radio del polígono. El radio de la circunferencia inscrita es el apotema del polígono.

Fórmulas

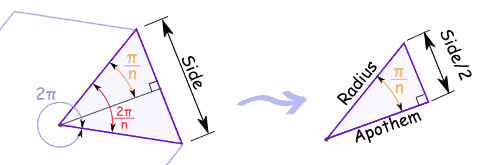
Si tomamos un "sector" de un polígono regular de "n" lados y lo cortamos por la mitad, tenemos un triángulo pequeño que contiene toda la información importante:

(Nota: los ángulos son en radianes, no en grados)

El triángulo pequeño es rectángulo así que podemos usar seno, coseno y tangente para ver las relaciones entre el lado, el radio, el apotema y "n":

sin(π/n) = (Lado/2) / Radio		Lado = 2 × Radio × sin(π/n)
cos(π/n) = Apotema / Radio		Apotema = Radio × cos(π/n)
tan(π/n) = (Lado/2) / Apotema		Lado = 2 × Apotema × tan(π/n)

Hay muchas más relaciones como estas (casi todas son "reordenamientos"), pero con estas nos vale por ahora.

Área

Ahora es fácil calcular el área... ¡sólo sumar las áreas de todos los triángulos!

El área de un triángulo es la mitad de la base por la altura, así que:

Área del triángulo pequeño = ½ × Apotema × (Lado/2)

Y sabemos (por la fórmula con "tan" de arriba) que:

Lado = 2 × Apotema × tan(π/n)

Así que:	Área del triángulo pequeño	= ½ × Apotema × (Apotema × tan(π/n))
		= ½ × Apotema2 × tan(π/n)

Y hay dos triángulos por lado, o sea 2n en todo el polígono:

Área del polígono = n × Apotema² × tan(π/n)

¡La verdad es que es una fórmula muy simple!

Otras fórmulas del área

Si no sabes cuánto mide el apotema, podemos sacar fórmulas con el radio y el lado:

Área del polígono = ½ × n × Radio² × sin(2 × π/n)

Área del polígono = ¼ × n × Lado² / tan(π/n)